Building a reversible sound change tool in Rust

A very long time ago, I came across rsca (reversible sound change applicator), a long-abandoned sound change tool written in C++. rsca lets the user build a model of the regular sound changes commonly found in the history of languages – something useful for doing historical linguistics ("given this list of sound changes, what would this Old English word look like in Modern English?") as well as in naturalistic conlanging ("how can I make 3 dialects of Space Elvish that plausibly derive from the same language").

The coolest thing about rsca was that unlike every other tool I've seen (including zompist's SCA2 tool, which is somewhat widely known in the conlanging community), rsca can reverse sound changes — given a list of sound changes, not only can it predict the form in the daughter language given a word in the parent language, it can reconstruct possible forms in the parent language given forms in the daughter language.

Unfortunately, rsca was very buggy and segfaulted half the time I tried to use it. It was unique enough of a tool that I attempted to fork it and fix the segfaults all the way back in 2014, but I eventually gave up.

But last year, I suddenly had the idea to reimplement a rsca-like tool (called premiena) in Rust, which would of course eliminate segfaults and make things easier to maintain. I also wanted to properly understand how rsca worked rather than slavishly copying its logic. This blogpost will touch on some interesting problems I encountered while implementing premiena.

Sound changes as NFSTs

rsca's seemingly magical superpower comes from representing sound changes with a particular formalism — nondeterministic finite state transducers (NFSTs). These are similar to the nondeterministic finite state automata (NFAs) used in regex engines and the like to recognize regular languages, except that a transducer not only consumes strings, but also produces an output as it does so. This means an NFST defines a relation between strings, rather than simply a set of strings.

For instance, this NFST replaces all instances of "N" with "n":

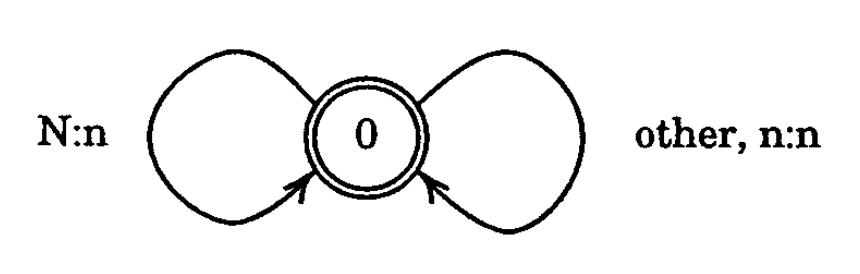
The foundational paper on formalizing sound changes as NFSTs seems to be Regular Models of Phonological Rule Systems by Kaplan and Kay, which gave a powerful argument that NFSTs and the regular relations they represent are the ideal model for sound changes. And by simply reversing input and output labels on a sound change representing NFST, we get a NFST that represents its reverse — making a reversible sound change applicator.

The most exciting thing about that paper is that not only does it show that NFSTs are the right formalism to represent sound changes, it does so constructively by presenting an algorithm to translate a conventionally represented sound change rule (such as "n -> m / _p", meaning n turns into m before p) into an NFST, based on algorithms for more basic actions like concatenating or taking the Kleene star of an NFST.

I was really happy to find this algorithm, so I went ahead to try to implement it, starting with the basic building blocks for working with both NFSTs (representing regular relations) and NFAs (representing regular languages).

Unfortunately, I quickly ran into a few roadblocks...

Roadblock 1: NFST composition

Kaplan and Kay's paper is very well-written, but one thing that I personally found difficult was the lack of any pseudocode combined with metaphors and formalisms that are highly "declarative" and hard to translate into code.

The biggest example of this was NFST composition — turning two NFST representing regular relations \(f\) and \(g\) into a single NFST representing the relation \(f \circ g\) — this can be used to make a single NFST that represents two sound changes, applied one after another. Here's how the paper presented this:

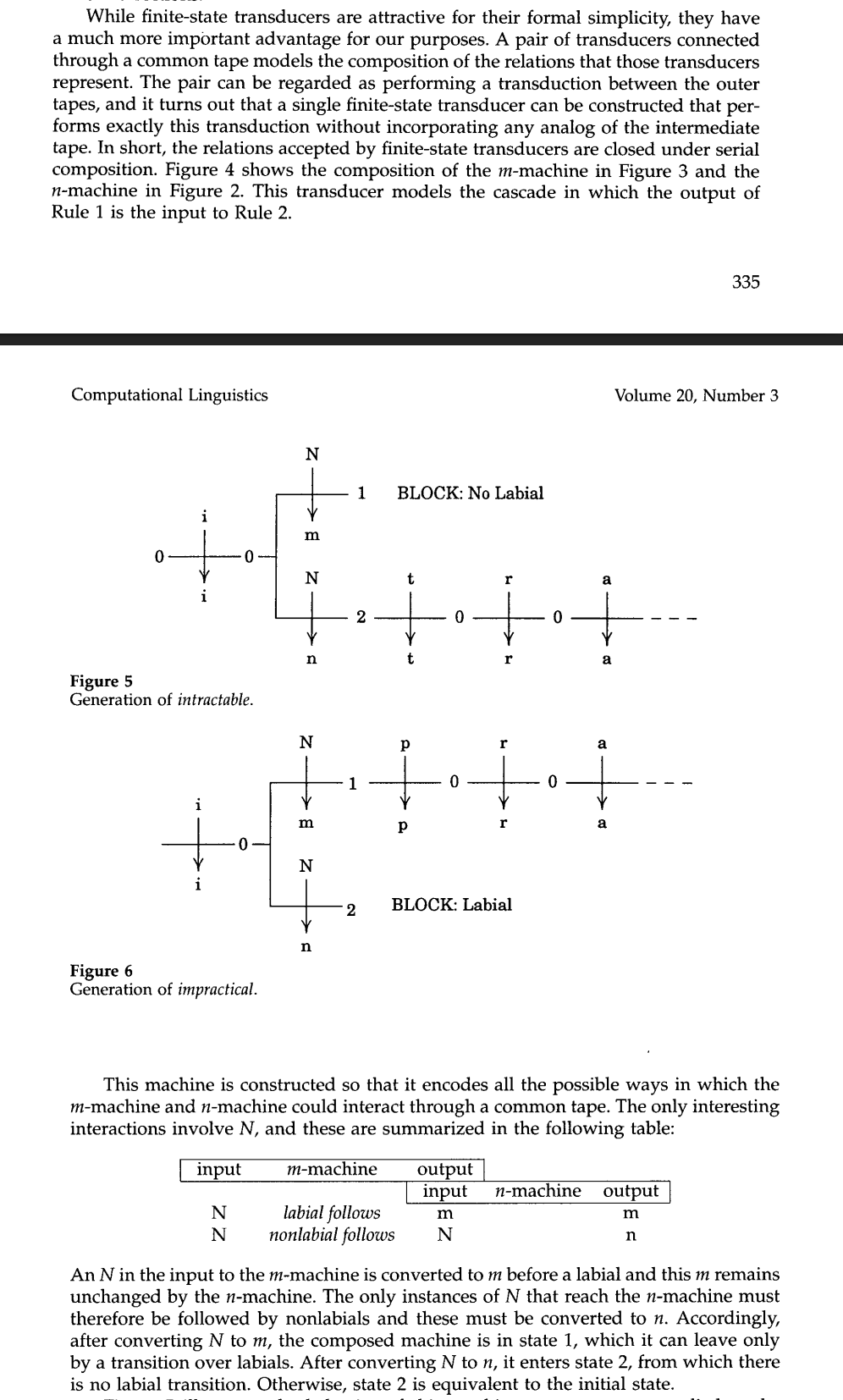
It uses an interesting "common tape" analogy, and notes that we don't actually need to model this tape, but unfortunately does not give an algorithm for constructing the transducer that "performs exactly this transduction without incorporating any analog of the intermediate tape".

By a lot of intense yet unhelpful Googling (people don't talk much about NFSTs online) I eventually was able to piece together a composition algorithm that seemed to work, though it was slower than I expected. Given a NFST with \(n\) transitions and another with \(m\) transitions, my algorithm would always produce one with \(nm\) transitions, so after composing a few NFSTs the result would blow up in size immensely.

Roadblock 2: recognizing the sound change context

The second roadblock I encountered happened when implementing the actual logic for constructing the NFST that corresponds to the sound changes. In the paper, the overall logic for translating a rule of the form \[ \phi \rightarrow \psi / \lambda \text{ __ } \rho \] involves constructing and then passing the input string through these transducers:

• \(\mathrm{Prologue}\), a transducer that inserts an arbitrary number of boundary symbols \(<,>\) into all positions in the string. For example, \(\mathrm{Prologue}\) applied to the string \(\mathsf{hello}\) produces the infinite regular language \(\{\mathsf{hello}, \textsf{h<ello}, \textsf{he<l>lo}, \dots \}\)
• \(\mathrm{Leftcontext}(\lambda,<.>)\), a regular language whose purpose is to filter the output of \(\mathrm{Prologue}\) so that the \(<\) marker only appears immediately after the left-side context of the sound change (\(\lambda\)), and \(\mathrm{Rightcontext}(\rho,<.>)\), which does the same for the right-hand-side. The effect here is to surround the sounds eligible for the sound change with brackets. For instance, if the sound change is \[ \textsf{ll} \rightarrow \textsf{y} / \textsf{e}\text{ __ }\textsf{o}\] (change all "ll" to "y" after "e" and before "o"), then \[\textsf{he<ll>o} \in \mathrm{Leftcontext}(\textsf{e}, <, >) \cup \mathrm{Rightcontext}(\textsf{o}, <, >) \] but \[\textsf{h<ell>o} \notin \mathrm{Leftcontext}(\textsf{e}, <, >) \cup \mathrm{Rightcontext}(\textsf{o}, <, >) \]
• \(\mathrm{Replace}(\phi, \psi\), a transducer that executes the replacement itself.
• \(\mathrm{Prologue}^{-1}\), which removes all the brackets from the output

The paper gives an excellent explanation on how these NFSTs are constructed, and when implemented following the paper, most of the NFSTs constructed seem to behave correctly (e.g. \(\mathrm{Prologue}\) does indeed insert brackets in the right places).

The only place where I got stuck was with the context operator. The paper gives this definition for \(\mathrm{Leftcontext}\):

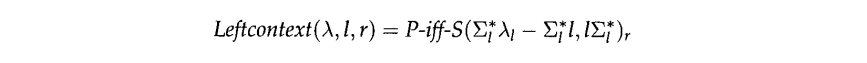
Note that:

• \(x_y\) read as "\(x\) ignore \(y\)", and meaning "the language where if you remove all instances of \(y\) in each string of the language, the resulting string is in \(x\)"
• \(\Sigma\) is the alphabet, which does not include \(l\) or \(r\))
• \(\textit{P-iff-S}(x,y)\) indicates the regular language where for every partition \(a||b\) of string in the language, \(a \in x\) and \(b \in y\)

Unfortunately, when I implemented this, it let through many strings that did not put the brackets in the right place. For example, for the sound change \[ \textsf{ll} \rightarrow \textsf{y} / \textsf{e}\text{ __ }\textsf{o}\] the left-context language would be \[ \textit{P-iff-S}(\Sigma^{*}_< \textsf{e}_< - \Sigma^{*}_< <,<\Sigma^{*}_<)_>\]

But such a left-context would accept incorrect strings like \(\textsf{h>ello}\), which does not contain left contexts at all. This is because \(\textsf{h>ello}\) is vacuously in \(\textit{P-iff-S}(\Sigma^{*}_< \textsf{e}_< - \Sigma^{*}_< <,<\Sigma^{*}_<)\), since it does not contain any prefix in \(\Sigma^{*}_< \textsf{e}_< - \Sigma^{*}_< <\) at all, since \(\Sigma\) does not include \(>\), but the only prefix that ends in \(\textsf{e}\) includes \(>\). And if the string is in \(\textit{P-iff-S}(\Sigma^{*}_< \textsf{e}_< - \Sigma^{*}_< <,<\Sigma^{*}_<)\), then by the definition of the "ignore" operator it's also in \(\textit{P-iff-S}(\Sigma^{*}_< \textsf{e}_< - \Sigma^{*}_< <,<\Sigma^{*}_<)_>\).

I think that this might be a mistake/ambiguity in the original paper. It seems like the intention here is to not include \(r\) in the alphabet of the language \(\textit{P-iff-S}(\Sigma^{*}_l \lambda_l - \Sigma^{*}_l l,l\Sigma^{*}_l)\).

After I fixed this by excluding all strings including \(r\) from the inner part of the left-context definition, everything worked. (WLOG, the same applies to the right context)

Roadblock 3: performance issues

Finally, everything works. Unfortunately, performance is so bad – especially that of NFST composition – that it was essentially impossible to fully generate a transducer for a sound change using the construction given in the paper that can then be applied to any string.

Instead, I ended up having to pass the input string piecemeal through the different pieces of the transducer. Even then, generating the pieces of the transducer took about half a second for a simple sound change, which I worked around by translating each sound change rule in parallel using the amazing rayon crate.

This gets me a tool that can load a pretty long sound change file and start applying sound changes, in a few seconds. But that's quite slow compared to tools using simple regex find-and-replace such as SCA2. At this point, I remembered that rsca, when it didn't segfault, was much faster than what I had written. So I dug into its code, and it didn't seem to construct the transducers using the formal definitions in the paper at all! I didn't find any expressions that corresponded to the mathematical definitions of left-context, right-context, etc, or any basic helper functions for tasks like taking the complement of an NFA or implementing the \(\textit{P-iff-S}\) function.

Instead, it seems like rsca directly builds transducers by piecing together states transitions for the different phases, which I guess would be much faster by sidestepping slow processes like composition.

Once I understand rsca's approach better, I will definitely update premiena to use it!